近年来,对于预训练、预训练模型的研究非常成功。所谓预训练,就是通过自监督学习的方式,学习无标签数据的表征。学习后得到的表征(Representation)可以作为输入用于各类下游任务(Downstream Task),如分类任务中。各类实验表明,预训练模型能够有效帮助完成机器学习中的各类下游任务,并在CV、NLP等领域的下游任务中取得了突破性进展。考虑到预训练模型的重要性和不完备性,马腾宇教授将通过自监督学习的预训练过程得到的模型称为Foundation Models。
对于预训练模型展现出的这些优良效果,马教授首先提出了三个问题:为什么Foundation Models能够展现对下游任务的帮助效果?在什么场景下Foundation Models能够展现对下游任务的帮助效果?Foundation Models对下游任务有帮助效果背后的原因是什么?
为了解答上述问题,马教授从自监督的对比学习切入,从理论出发,通过研究预训练过程中被提取出的数据特征的结构,完成对于上述问题的理论分析;并以此为立足点,设计新的算法来帮助解决现有的域适应(Domain Adaptation)问题和分布外(Out of Domain,OOD)泛化的鲁棒性问题。
在对比学习中,模型的训练首先利用原始图片数据生成增强(Augmentation)后的图片数据集合。由于希望模型学习到同一个原始图片的不同增强图片数据是相似的,而不同图片生成的增强图片数据是不相似的,所以希望模型对于相似的图片输出的表征(Representation)尽可能相互靠近(图中红色箭头),而不相似的图片的表征尽可能相互远离(图中蓝色箭头)。这就带来了一个问题:如上定义的目标中,会使得两张有着相同的类别特征的数据(例如,两张狗的图片)生成的增强图片数据的表征可能在表征空间中相互远离。然而实际实验结果表明,上述问题几乎不会发生。
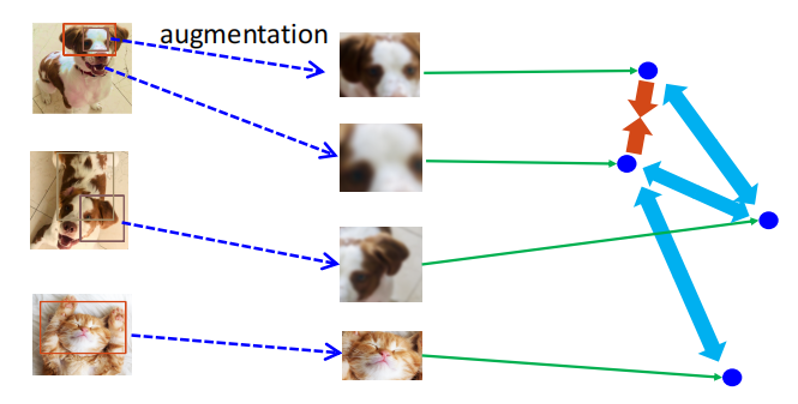
为了解释这个现象,马腾宇教授引入了正对图(Positive Pair Graph)上的谱聚类(Spectral Clustering)的概念。正对(Positive Pair),就是由同一个原始图片数据生成的两个不同的增强图片数据构成的数据对。如果将每一个增强图片数据作为图的顶点(node),同一个原始图片数据生成的不同的增强图片数据之间两两连接一条边(edge),就构成了一个正对图。
他希望一个谱聚类之后的正对图能够满足:不相似的原始图片数据生成的增强图片数据对应的顶点之间只有很少的边、相似的原始图片数据生成的增强图片数据对应的顶点之间则存在很多边。即,正对图的谱聚类的结果中各个聚类之间连接很少,但是同一个聚类内部顶点之间的连接更多。因此,可以认为谱聚类之后的正对图中,顶点之间的距离含有语义信息(Semantic Meaning)。当两个顶点的语义信息之间有相关性时(构成正对时),可以在正对图中找到一个有限长度的路径(path)连接两个顶点,即两个顶点之间的距离是有限的,一个顶点对应的增强数据可以沿着这条路径变换得到另一个顶点的数据,而且过程中变换得到的图片是可能真实存在的;否则,不存在语义关联的顶点(例如:分属不同类别的两个原始数据生成的增强数据对应的顶点)之间距离是无限的。
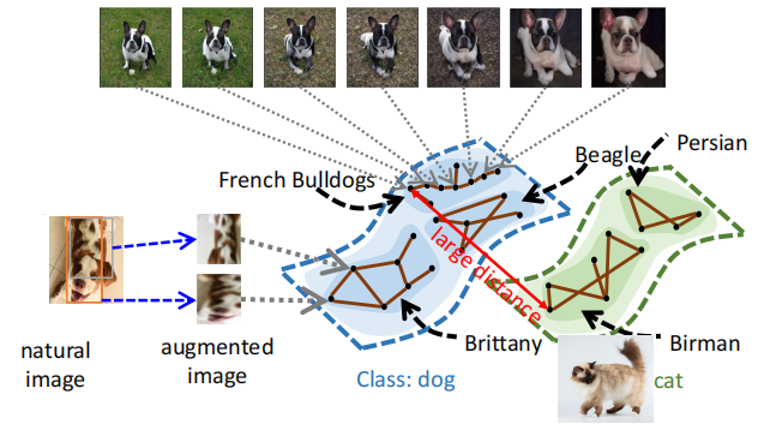
出于上述期望,马腾宇教授团队定义了一种新型的对比学习中的损失函数,称为谱对比损失函数(Spectral Contrastive Loss)。该损失函数希望在完成正对图的谱聚类时,正对的表征(f(x))尽量相近,而非正对(Random Pair)的表征之间尽可能相互远离。
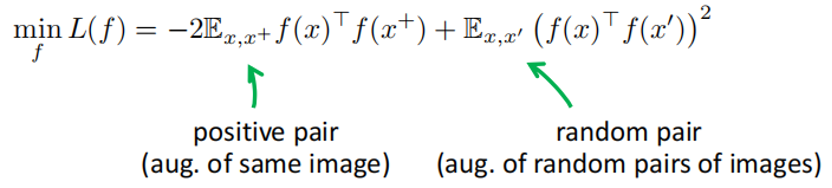
该损失函数不仅在理论分析中有很好的特性,而且大量实验表明,它在实际中也有很好的效果,与SOTA方法有着相同的实验效果。马教授团队据此提出,最小化谱对比损失函数等价于在正对图上完成谱聚类任务。也因此,正对图上完成谱聚类任务结束后,属于同一个类型的原始数据生成的增强数据之间的距离在表征空间中相互靠近。

然而,上述理论分析没有解释为什么自监督的对比学习任务可以提升下游任务,尤其是下游线性任务的效果。也没有解释自监督的对比学习任务可以解决什么样类型的下游任务。通过理论分析,马腾宇教授提出,当谱聚类结果中的每个聚类(Cluster)中的数据在下游任务中拥有相同的标签(Label)时,对聚类后的表征(Representation)进行线性分类可以解决该下游任务。

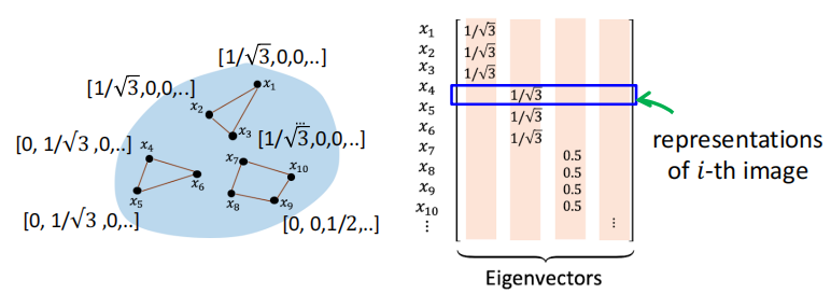
此外,自监督对比学习任务可以提升下游线性任务的效果是因为,谱聚类结果中每个顶点的表征(Representation)构成的矩阵的特征向量(Eigen Vector)代表了每个顶点所属的聚类。
在介绍完相关的正对图的谱聚类理论后,马腾宇教授介绍了两个由该理论启发的算法。
算法一是基于预训练的域适应(Domain Adaptation)算法SwAV。首先,通过观察发现,谱对比损失函数(Spectral Contrastive Loss)也能捕获聚类(Cluster)之间的关系。如下图所示,四个聚类类别(从上到下、从左到右)分别属于草图蝴蝶、草图钟表、实物图蝴蝶、实物图钟表。其中,草图的数据属于同一个域(Domain),实物图的数据属于同一个域(Domain)。而蝴蝶和钟表是两个不同的分类类别(Class)。当选用合适的正对图进行合适的谱聚类后,由上述理论可以知道:在谱聚类得到的表征空间中,这四个聚类线性可分(Linear Separable)。虽然无法确定每个聚类出现在空间中的具体位置,但是可以知道这些聚类之间的位置存在线性可分性(Linear Separability)。这是因为属于每个域中同一类别的数据顶点之间的边(图中黑色边)的数量远大于不同域和/或不同类别的顶点之间的边(图中粉色边/蓝色边)的数量。
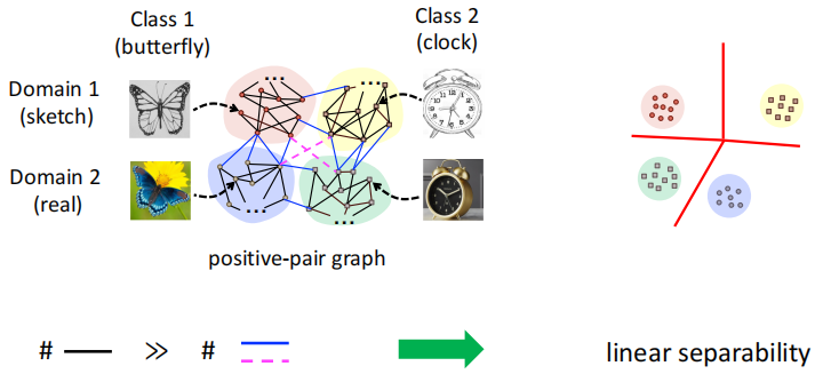
与此同时,由于图中蓝色边的数量远大于图中粉色边的数量,因此同域不同类别(或同类别不同域)的顶点之间的关联性远强于不同域不同类别之间点的关联性。这为无监督的域适应算法(SwAV)提供了理论基础。
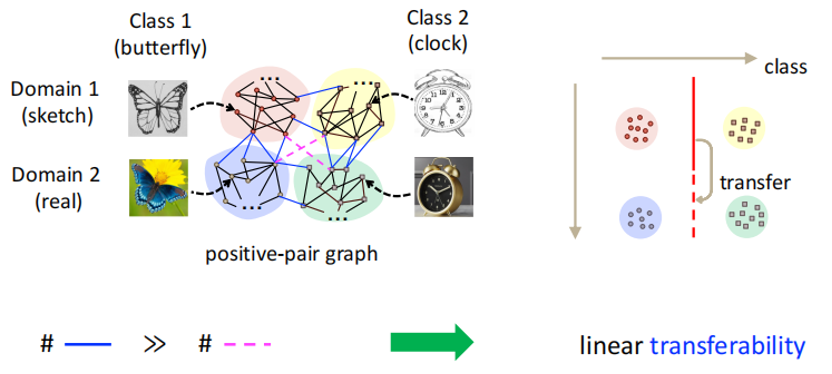
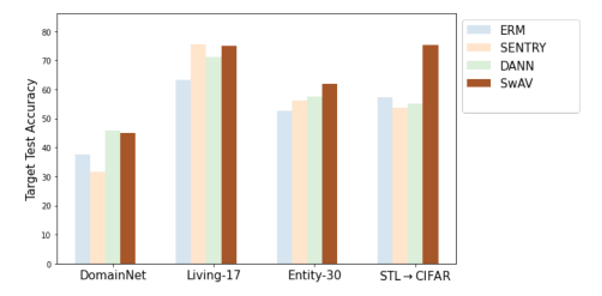
SwAV算法为:在两个域(来源域和目标域)的全部数据上完成预训练(Pre-train on Unlabeled Data from Source-Target Combined Domain),并在草图域(来源域,Source Domain)上完成有监督的蝴蝶、钟表的线性分类任务的微调(Fine-tune on Labeled Data from Source Domain),最终结果可以完成对于无监督的实物图域(目标域,Target Domain)上蝴蝶、钟表的线性分类任务(Evaluate on Data from Target Domain),即完成无监督的域适应(Unsupervised Domain Adaptation)。该性质可称为线性迁移性(Linear Transferability)。实验表明,该算法下,目标域上的分类效果可以达到甚至超过SOTA方法(DANN等)的分类效果。
更进一步,如果允许使用额外的数据一同进行无监督的预训练过程,SwAV算法的效果会更上一层楼(下图SwAV+Extra所示)。
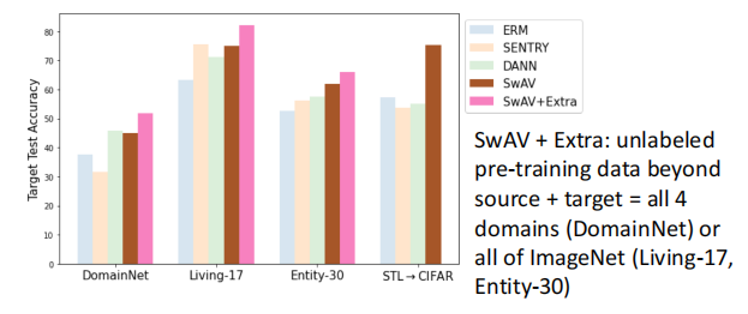
需要注意到,不同于DANN等算法,SwAV算法成功的关键不是将两个不同域上数据的表征相互融合、靠近,以使得两个域的数据在表征空间中无法区分。相反,相较于DANN算法,SwAV算法下,各个域之间的表征相差更远。

算法二是为提升分布外(Out of Domain,OOD)泛化鲁棒性的微调(Fine-tune)算法PL-FT。
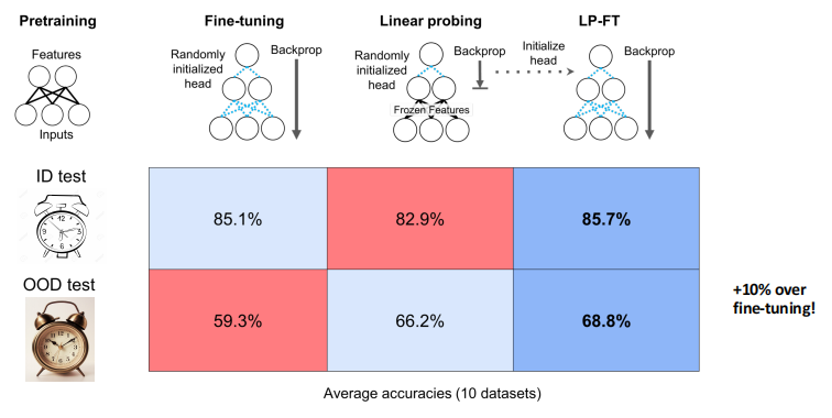
相较于前一个算法的使用场景,该算法适用于目标域数据缺失的情况。该情境下,常用的预训练-微调(Pre-train + Fine-tune)算法步骤为:在大规模无标签数据集上进行预训练(Pre-train on Large-scale Unlabeled Data),并在来源域上完成有监督的微调(Fine-tune on Labeled Data from Source Domain),最后在少量目标域数据上进行评价(Evaluate on Data from Target Domain)。该算法的问题是,不同的微调方法在不同的数据分布上有着不一样的表现。常用的两种微调方法,全参数微调(Fine-tune)在目标域和来源域数据同分布(ID)时通常表现优于仅调整线性头(Linear Head)的线性探测(Linear Probe)的方法;而当目标域和来源域数据拥有不同分布(OOD)时,线性探测通常拥有更好的表现。
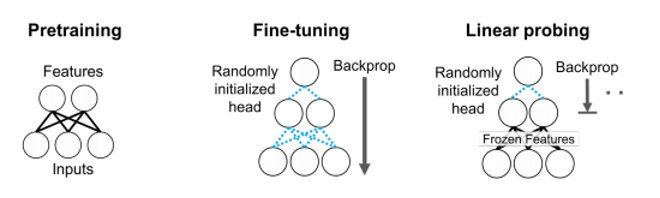
马教授用特征扭曲理论(Feature Distortion Theory)来解释这种现象。如下图(1)(2)所示,在全参数微调时,线性头(Linear Head)调整较少、数据特征调整更多的可能会使得全参数微调在面对不同分布(OOD)数据时不鲁棒,但是面对同分布(ID)数据时表现优异。而线性探测因为仅仅调整线性头,所以不存在上述风险,因此对不同分布(OOD)数据鲁棒性更佳。
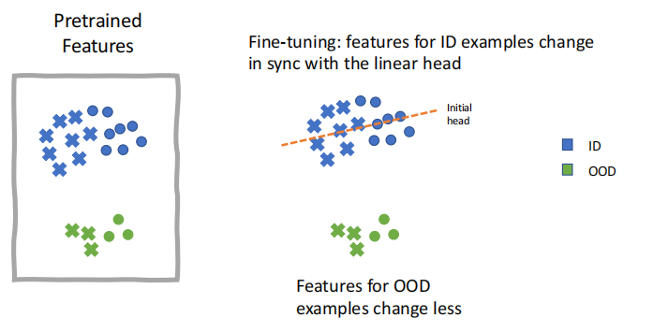
图示(1)
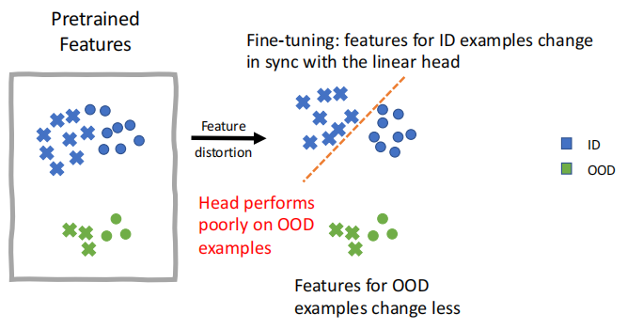
图示(2)
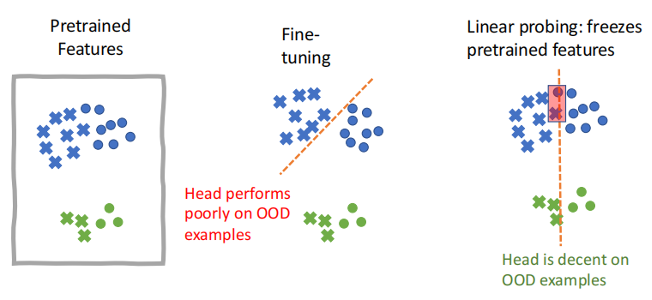
图示(3)
通过上述观察,为了平衡上述数据特征和线性头之间的调整程度,马腾宇教授团队提出了LP-FT的微调方法:先通过线性探测(Linear Probe,LP)调整得到合适的线性头;再通过全参数微调(Fine-tune,FT)完成对于数据特征的调整。以此达到微调数据表征但是不会过度调整的效果。实验结果表明,LP-FT微调方法在ID和OOD数据任务上都有很好的效果。尤其是在预训练得到数据表征较好且OOD的域间差距较大时,LP-FT相较FT有着非常明显的效果提升。
上述两种由理论启发的算法都在实际应用中展现出了良好的效果。而在最后的问答环节中,马腾宇教授也表达了自己对于理论研究的观点:从长远的角度看,理论研究的意义在于启发新的、有效的算法。
文稿撰写 / 邹恬圆
排版编辑 / 张子瞻
校对责编 / 黄 妍


